Doppler spectroscopy

Doppler spectroscopy, also known as radial velocity measurement, is a spectroscopic method for finding extrasolar planets. It involves the observation of Doppler shifts in the spectrum of the star around which the planet orbits.

It is extremely difficult to directly observe extrasolar planets because they are very faint at interstellar distances, although the first claims of direct observations were made in 2004 and 2005. As a result, planets outside of our solar system are usually discovered using indirect methods, through the effect of the planet on an object that is easier to observe, such as the parent star. Successful methods include Doppler spectroscopy, astrometry, pulsar timing, transits, and gravitational microlensing. As of September 15, 2011, over 90% of the known extrasolar planets have been discovered using Doppler spectroscopy.[1]

Contents

History

Otto Struve proposed in 1952 the use of powerful spectrographs to detect distant planets. He described how a very large planet, as large as Jupiter, for example, would cause its parent star to wobble slightly as the two objects orbit around their center of mass.[2] He predicted that the small Doppler shifts to the light emitted by the star, caused by its continuously varying radial velocity, would be detectable by the most sensitive spectrographs as tiny red shifts and blue shifts in the star's emission. However, the technology of the time produced radial velocity measurements with errors of 1,000 m/s or more, making them useless for the detection of orbiting planets.[3] The expected changes in radial velocity are very small – Jupiter causes the Sun to change velocity by about 13 m/s over a period of 12 years, and the Earth's effect is only 0.1 m/s over a period of 1 year – so long-term observations by instruments with a very high resolution are required.[3][4]

Advances in spectrometer technology and observational techniques in the 1980s and 1990s produced instruments capable of detecting the first of many new extrasolar planets. 51 Pegasi b, the first extrasolar planet to be detected, was discovered in October 1995 using Doppler spectroscopy.[5] Since that date, nearly 300 exoplanet candidates have been identified, and most have been detected by Doppler search programs based at the Keck, Lick, and Anglo-Australian Observatories (respectively, the California, Carnegie and Anglo-Australian planet searches), and teams based at the Geneva Extrasolar Planet Search.[5]

The Bayesian Kepler periodogram is a mathematical algorithm, used to detect single or multiple extrasolar planets from successive radial velocity measurements of the star they are orbiting. It involves a Bayesian statistical analysis of the radial velocity data, using a prior probability distribution over the space determined by one or more sets of Keplerian orbital parameters. This analysis may be implemented using the Markov chain Monte Carlo (MCMC) method.

The method has been applied to the HD 208487 system, resulting in an apparent detection of a second planet with a period of approximately 1000 days. However, this may be an artifact of stellar activity.[6][7] The method is also applied to the HD 11964 system, where it found an apparent planet with a period of approximately 1 year. However, this planet was not found in re-reduced data,[8][9] suggesting that this detection was an artifact of the Earth's orbital motion around the Sun.

Procedure

A series of observations is made of the spectrum of light emitted by a star. Periodic variations in the star's spectrum may be detected, with the wavelength of characteristic spectral lines in the spectrum increasing and decreasing regularly over a period of time. These variations may be indicative of the radial velocity of the star being altered by the presence of planet orbiting the star, causing Doppler shifts in the light emitted by the star.

If an extrasolar planet is detected, its mass can be determined from the changes in the star's radial velocity. A graph of measured radial velocity versus time will give a characteristic curve (sine curve in the case of a circular orbit), and the amplitude of the curve will allow the planet's mass to be calculated.

Example

The graph to the right illustrates the sine curve created using Doppler spectroscopy to observe the radial velocity of an imaginary star which is being orbited by a planet in a circular orbit. Observations of a real star would produce a similar graph, although eccentricity in the orbit will distort the curve and complicate the calculations below.

This theoretical star's velocity shows a periodic variance of ±1 m/s, suggesting an orbiting mass that is creating a gravitational pull on this star. Using Kepler's third law of planetary motion, the observed period of the planet's orbit around the star (equal to the period of the observed variations in the star's spectrum) can be used to determine the planet's distance from the star (r) using the following equation:

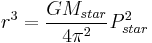
r^3=\frac{GM_{star}}{4\pi^2}P_{star}^2\,

where:

Having determined r, the velocity of the planet around the star can be calculated using Newton's law of gravitation, and the orbit equation:

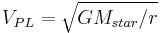
V_{PL}=\sqrt{GM_{star}/r}\,

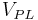where V_{PL} is the velocity of planet.

The mass of the planet can then be found from the calculated velocity of the planet:

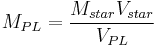
M_{PL}=\frac{M_{star}V_{star}}{V_{PL}}\,

where 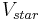V_{star} is the velocity of parent star. The observed Doppler velocity, 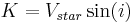K = V_{star}\sin(i), where i is the inclination of the planet's orbit to the line perpendicular to the line-of-sight.

Thus, assuming a value for the inclination of the planet's orbit and for the mass of the star, the observed changes in the radial velocity of the star can be used to calculate the mass of the extrasolar planet.

Radial velocity comparison tables

Planets[10]
Planetary mass Distance
(AU)		 Radial velocity
(m/s)
Jupiter 1 28.4
Jupiter 5 12.7
Neptune 0.1 4.8
Neptune 1 1.5
Super-Earth (5 M⊕) 0.1 1.4
Super-Earth (5 M⊕) 1 0.45
Earth 1 0.09
MK-type stars with planets in the habitable zone[11]
Stellar mass
(M☉)		 Planetary mass
(M⊕)		 Lum.
(L0)		 Type RHAB
(AU)		 RV
(cm/s)		 Period
(days)
0.10 1.0 8×10−4 M8 0.028 168 6
0.21 1.0 7.9×10−3 M5 0.089 65 21
0.47 1.0 6.3×10−2 M0 0.25 26 67
0.65 1.0 1.6×10−1 K5 0.40 18 115
0.78 2.0 4.0×10−1 K0 0.63 25 209


Problems

The major problem with Doppler spectroscopy is that it can only measure movement along the line-of-sight, and so depends on a measurement (or estimate) of the inclination of the planet's orbit to determine the planet's mass. If the orbital plane of the planet happens to line up with the line-of-sight of the observer, then the measured variation in the star's radial velocity is the true value. However, if the orbital plane is tilted away from the line-of-sight, then the true effect of the planet on the motion of the star will be greater than the measured variation in the star's radial velocity, which is only the component along the line-of-sight. As a result, the planet's true mass will be higher than expected.

To correct for this effect, and so determine the true mass of an extrasolar planet, radial velocity measurements must be combined with astrometric observations, which track the movement of the star across the plane of the sky, perpendicular to the line-of-sight. Astrometric measurements allows researchers to check whether objects that appear to be high mass planets are more likely to be brown dwarfs.[3]

A further problem is that the gas envelope around certain types of stars can expand and contract, and some stars are variable. This method is unsuitable for finding planets around these types of stars, as changes in the stellar emission spectrum caused by the intrinsic variability of the star can swamp the small effect caused by a planet.

The method is best at detecting very massive objects close to the parent star — so-called "hot Jupiters" – which have the greatest gravitational effect on the parent star, and so cause the largest changes in its radial velocity. Observation of many separate spectral lines and many orbital periods allows the signal to noise ratio of observations to be increased, increasing the chance of observing smaller and more distant planets, but planets like the Earth remain undetectable with current instruments.

See also

References

  1. ^ Schneider, Jean (10 September 2011). "Interactive Extra-solar Planets Catalog". The Extrasolar Planets Encyclopedia. http://exoplanet.eu/catalog.php. Retrieved 2011-09-10. 
  2. ^ O. Struve (1952). "Proposal for a project of high-precision stellar radial velocity work". The Observatory 72 (870): 199–200. Bibcode 1952Obs....72..199S. 
  3. ^ a b c "Radial velocity method". The Internet Encyclopedia of Science. http://www.daviddarling.info/encyclopedia/R/radial_velocity_method.html. Retrieved 2007-04-27. 
  4. ^ A. Wolszczan (Spring 2006). "Doppler spectroscopy and astrometry – Theory and practice of planetary orbit measurements" (PDF). ASTRO 497: "Astronomy of Extrasolar Planets" lectures notes. Penn State University. http://www.astro.psu.edu/users/alex/astro497_2.pdf. Retrieved 2009-04-19. 
  5. ^ a b R.P. Butler et al. (2006). "Catalog of Nearby Exoplanets" (PDF). Astrophysical Journal 646 (2–3): 25–33. http://exoplanets.org/cne.pdf. 
  6. ^ P.C. Gregory (2007). "A Bayesian Kepler periodogram detects a second planet in HD 208487". Monthly Notices of the Royal Astronomical Society 374 (4): 1321–1333. arXiv:astro-ph/0609229. Bibcode 2007MNRAS.374.1321G. doi:10.1111/j.1365-2966.2006.11240.x. 
  7. ^ Wright et al.; Marcy, G. W.; Fischer, D. A; Butler, R. P.; Vogt, S. S.; Tinney, C. G.; Jones, H. R. A.; Carter, B. D. et al. (2007). "Four New Exoplanets and Hints of Additional Substellar Companions to Exoplanet Host Stars". The Astrophysical Journal 657 (1): 533–545. arXiv:astro-ph/0611658. Bibcode 2007ApJ...657..533W. doi:10.1086/510553. http://www.iop.org/EJ/article/0004-637X/657/1/533/65907.html. 
  8. ^ P.C. Gregory (2007). "A Bayesian periodogram finds evidence for three planets in HD 11964". Monthly Notices of the Royal Astronomical Society 381 (4): 1607–1616. Bibcode 2007MNRAS.381.1607G. doi:10.1111/j.1365-2966.2007.12361.x. 
  9. ^ J.T. Wright et al. (2008). "Ten New and Updated Multi-planet Systems, and a Survey of Exoplanetary Systems". The Astrophysical Journal 693 (2): 1084–1099. arXiv:0812.1582. Bibcode 2009ApJ...693.1084W. doi:10.1088/0004-637X/693/2/1084. 
  10. ^ "ESPRESSO and CODEX the next generation of RV planet hunters at ESO". Chinese Academy of Sciences. 2010-10-16. http://202.127.29.4/bdep_meeting/download/talks/20July/10-LPasquini.ppt. Retrieved 2010-10-16. 
  11. ^ "An NIR laser frequency comb for high precision Doppler planet surveys". Chinese Academy of Sciences. 2010-10-16. http://202.127.29.4/bdep_meeting/download/talks/20July/SOsterman.pptt. Retrieved 2010-10-16. 

External links